Inbreeding is the probability that an individual inherits two identical alleles from a common ancestor (Falconer and Mackay, 1996). There are several ways to obtain inbreeding coefficients using pedigree or genomic information. One method is via the diagonal elements of the genetic relationship matrix.
Let A be the numerator (pedigree) relationship matrix and $a_{ii}$ its ith diagonal element. The inbreeding coefficient of the ith animal is:
$$ F_i = a_{ii} - 1. $$
The diagonal elements of A have a one-tailed distribution with a minimum of 1. When calculating inbreeding coefficients from the diagonal elements of the genomic relationship matrix (G):
$$ F_i = g_{ii} - 1, $$
some coefficients are negative because the diagonal elements of G have a two-tailed, right-skewed distribution, with some values less than 1.
Here, I introduce weights to scale G so that the minimum of its diagonal values becomes 1, while preserving the maximum. This scaling ensures that an animal’s genetic relationship with itself (i.e., the diagonal element of G) cannot fall below 1, and the inbreeding coefficient cannot be less than 0.
Let vector g contain the $g_{ii}$ elements (the diagonal elements of G). Multiplying each $g_{ii}$ by weight $w_i$ scales g to the range [1, max(g)], where
$$ w_i = \frac{\frac{(g_{ii} - \text{min}(\mathbf g)) (\text{max}(\mathbf g) - 1)}{\text{max}(\mathbf g) - \text{min}(\mathbf g)} + 1}{g_{ii}}. $$
Collating the $w_i$ elements into vector w, its values range from $1 / \min(\mathbf g)$ (applied to $\min(\mathbf g)$) to 1 (applied to $\max(\mathbf g)$).
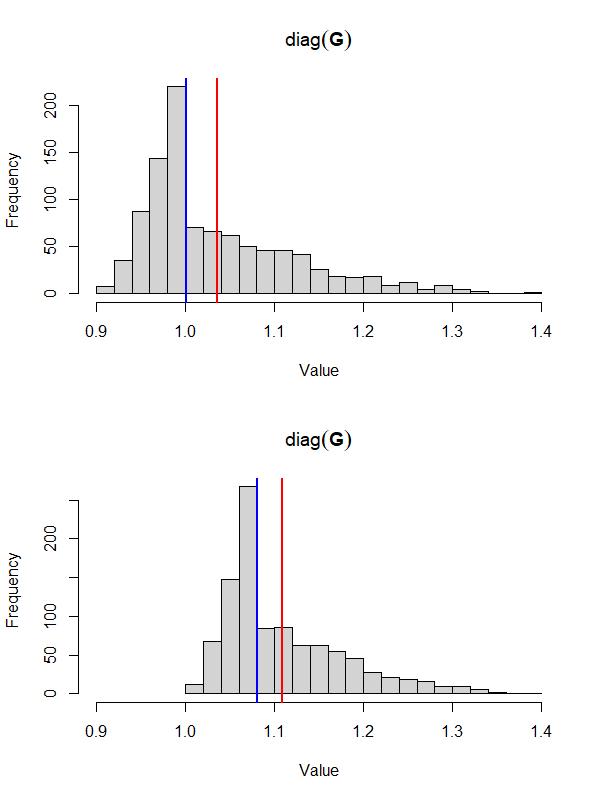
The following plots show the distribution of diag(G) before and after scaling. The blue line shows the median; the red line shows the mean.
If the full matrix G is required, the remaining elements should also be scaled. This can be done by multiplying:
$$ \sqrt{\mathbf W} \mathbf G \sqrt{\mathbf W}, $$
where W is a diagonal matrix of the $w_i$ elements. Using such G in a genetic evaluation, the heritability should be multiplied to $\sum_{i=1}^n \sum_{j=1}^n g_{ij} / \sum_{i=1}^n \sum_{j=1}^n g_{ij} \sqrt{w_i w_j}$ to keep the genetic variance constant.